Pattern matching with the Aho-Corasick algorithm

In our homebrew legacy content management system at work, we have a sort of glossary that is used to enhance the content for the end user by autolinking words and phrases throughout the content. This is currently done in the backend after the content has been published.

In the new version of the system, we want to be able to show editors which words will be autolinked by the backend service as they are editing the content, for better visibility and control. Because this will be done on the client side, I needed to find an efficient way to search for a list of strings in a large body of text, and that’s when I came across the Aho-Corasick algorithm.

The Aho-what?

The Aho-Corasick algorithm, invented by Alfred V. Aho and Margaret J. Corasick in 1975, is a way of finding multiple patterns in a text by constructing a data structure called trie where each node represents a letter of a word, and adding failure links to make navigation between nodes more efficient. The algorithm starts at the beginning of the text we want to search for patterns, and follows the trie as it reads each letter. If it gets to the end of a word in the trie, it means the pattern has been found in the text.

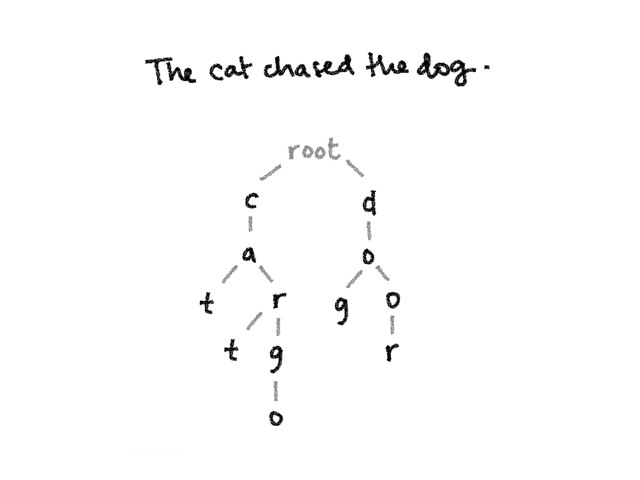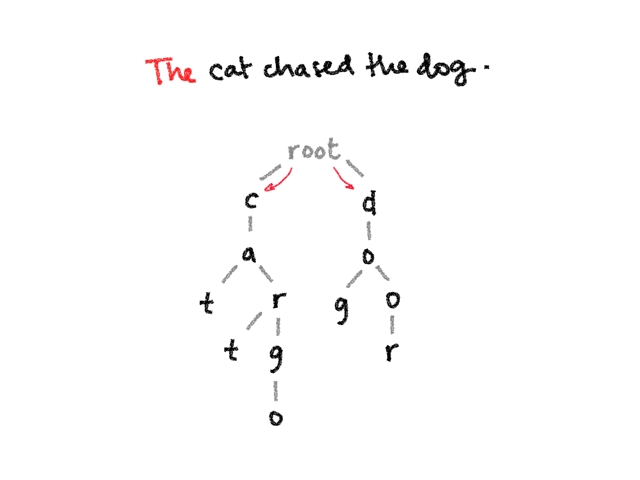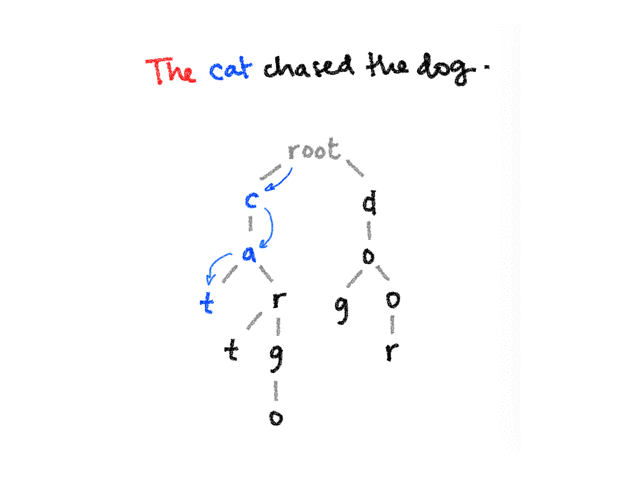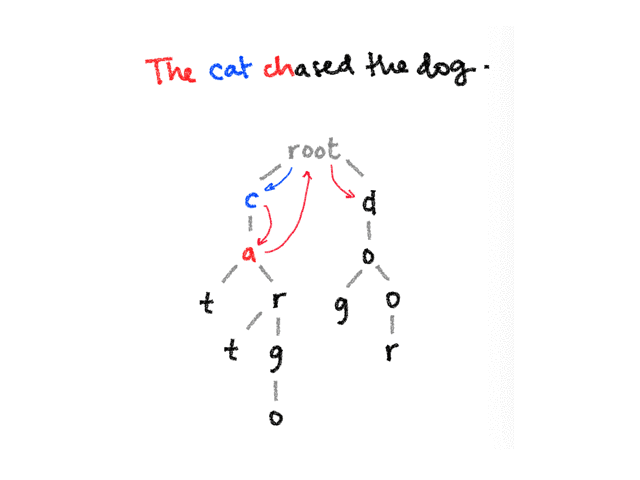
What’s a Trie?

A trie, also known as prefix tree, is a tree-like data structure that can be used to check if a particular combination of characters can be found in a set of strings. It starts from a root and each node represents the first letter of a string in the set we’re looking at, with subsequent child nodes representing the letter that comes after that.

For example, a trie for the words cat, car, cart, cargo, dog and door would look like this:

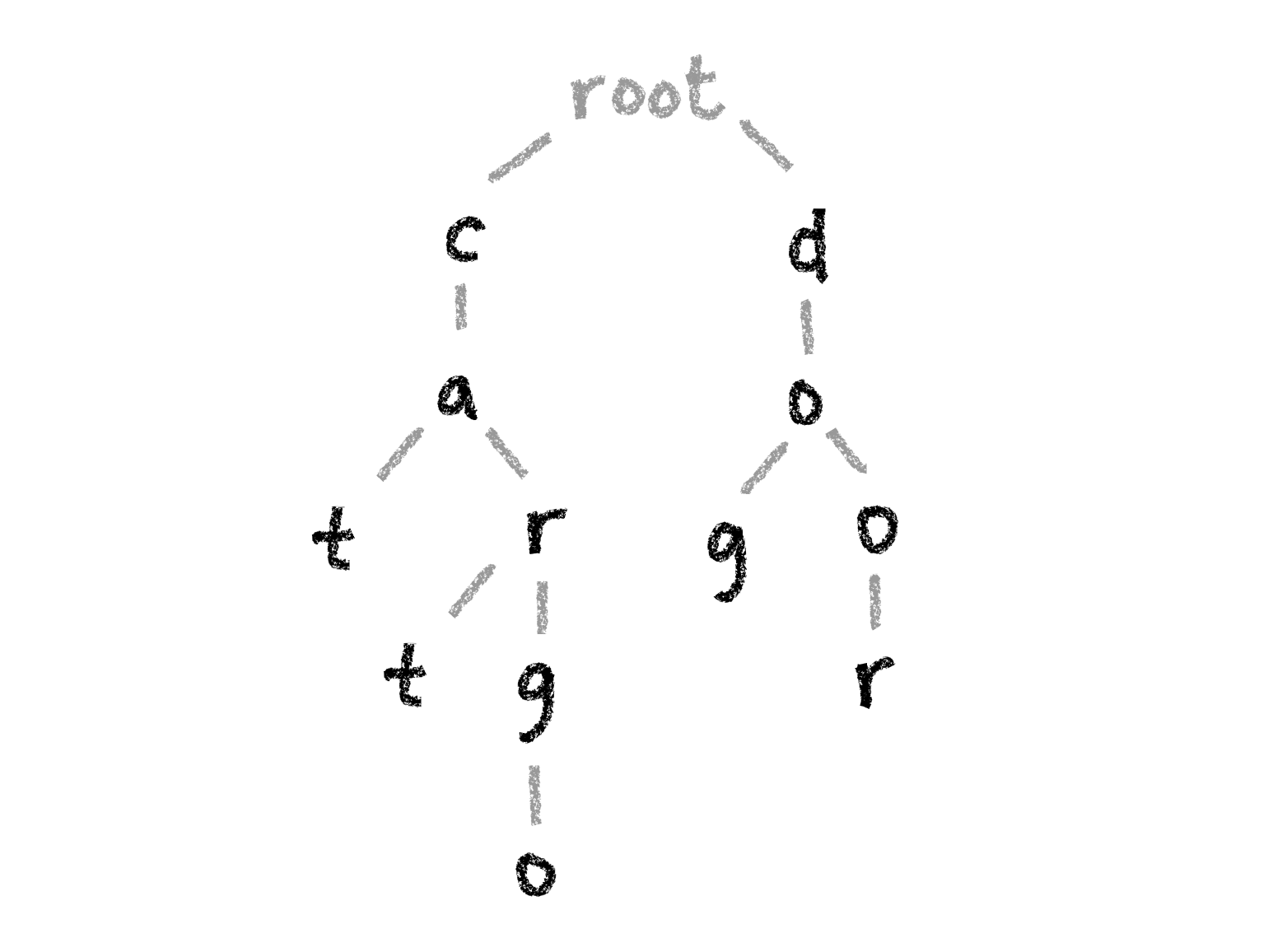
The nodes representing the last character of each string are marked so we can identify which words are actually part of the set.

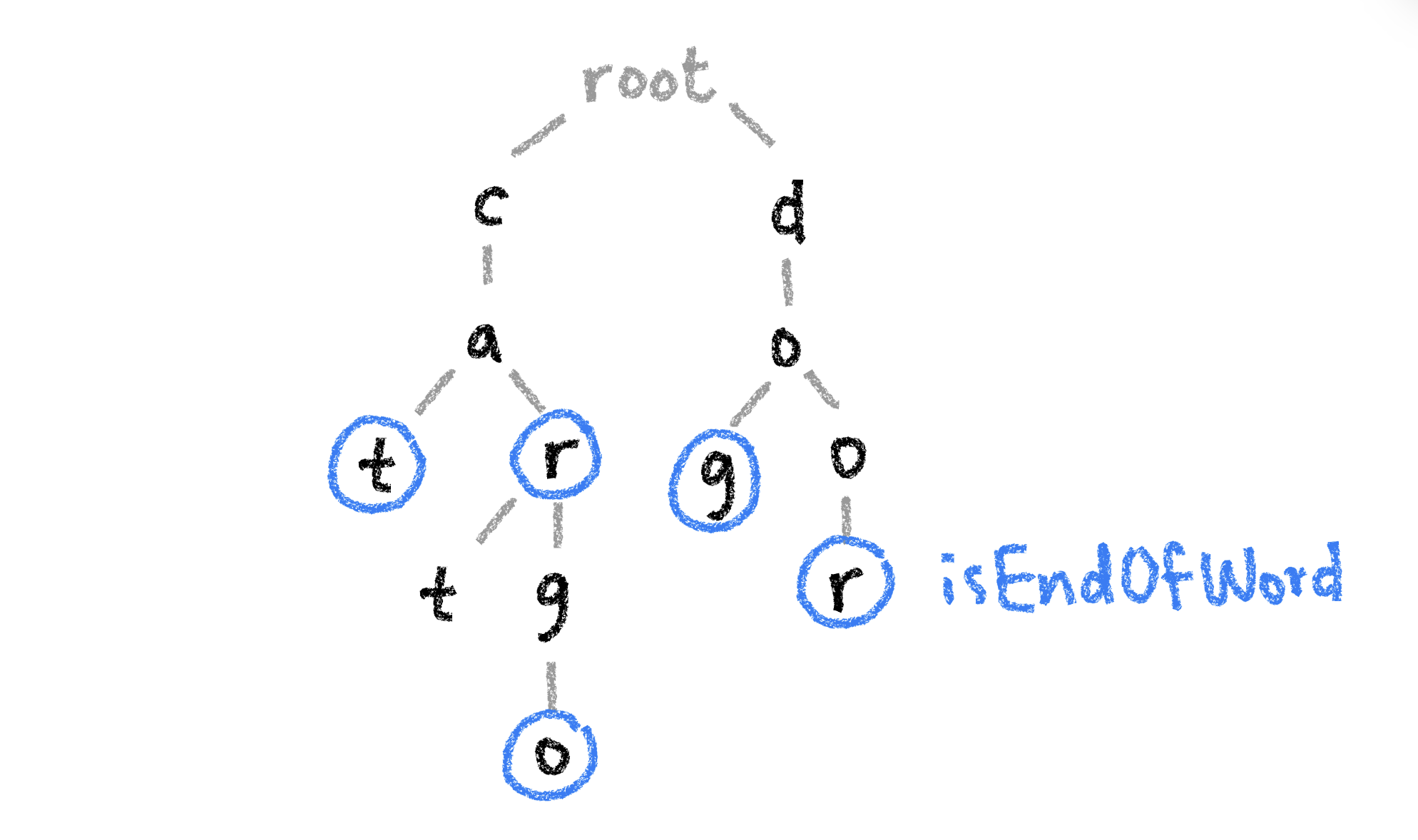
This data structure is a good way to store information because it makes operations like inserting, deleting and searching pretty fast, and it also scales well because it doesn’t matter how big your set is, finding the same string will always follow the same path and take the same number of operations.

Alright, enough theory, let’s see how we can implement this with Typescript:

1. Building a Trie

We’ll start by defining a Typescript interface to represent our data structure and the functions to create a trie and to insert patterns into it:

interface TrieNode {
	children: Map<string, TrieNode>
	isEndOfWord: boolean
	// stores which patterns end at this node for easier retrieval
	output: string[]
}

function createTrie(): TrieNode {
	return {
		children: new Map(),
		isEndOfWord: false,
		output: [],
	}
}

function insertPattern(root: TrieNode, pattern: string) {
	// create a copy so that we can traverse down the trie
	let rootNode = root

	// iterate over each character of a pattern
	for (const char of pattern) {
		// if the current character is not a child of the current node
		if (!rootNode.children.has(char)) {
			// create a new node and add it as a child of the current node
			rootNode.children.set(char, createTrie())
		}

		// point to the next node in the trie before
		// the following iteration
		rootNode = rootNode.children.get(char)!
	}

	// if the pattern already exists in the trie, but it didn't end
	// at the same character, mark this point as the end of a word
	if (!rootNode.isEndOfWord) {
		rootNode.isEndOfWord = true
		rootNode.output.push(pattern)
	}
}

2. Adding failure links

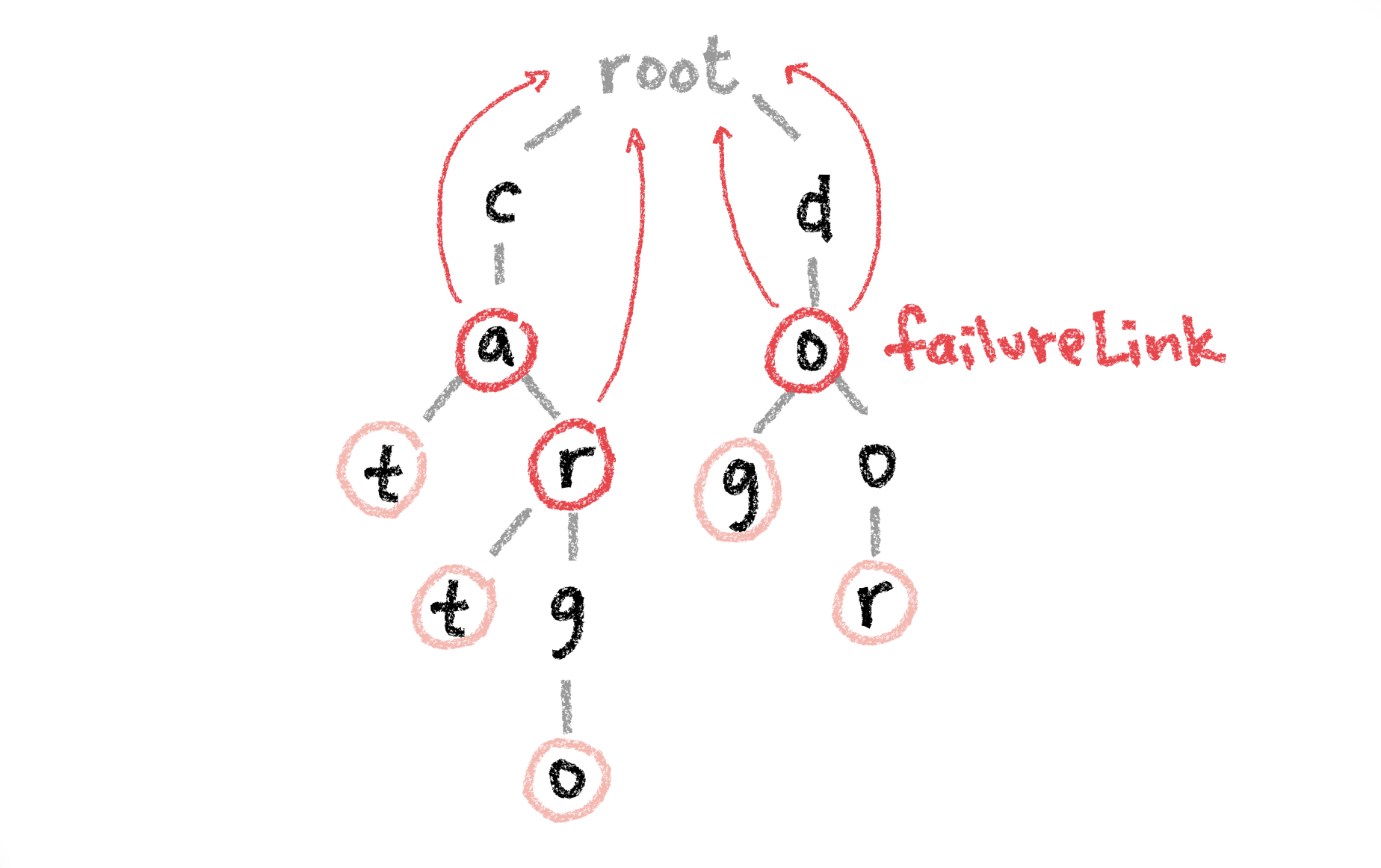
Then we need to enhance the trie by adding markers to allow for faster transitions between failed matches. Using our example words cat, car, cart, cargo, dog and door, if we try to search for the word cab, the search would fail on the first pass through c-a. Instead of having to backtrack to the beginning of the string, we can tell it to directly link to the first node to look for another branch that shares a common prefix.

interface TrieNode {
	// ...
	failureLink?: TrieNode
}

function addFailureLinks(root: TrieNode) {
	const queue: TrieNode[] = []

	// initialize failure links for first level nodes with the root node
	for (const child of root.children.values()) {
		child.failureLink = root
		queue.push(child)
	}

	// breadth-first search to add failure links
	while (queue.length > 0) {
		const currentNode = queue.shift()

		if (!currentNode) {
			break
		}

		for (const [char, child] of currentNode.children) {
			queue.push(child)

			let failureNode = currentNode.failureLink

			// if the current child is not a child of the node's failure link
			// then continue traversing to the next failure link
			while (failureNode !== root && !failureNode?.children.has(char)) {
				failureNode = failureNode?.failureLink
			}

			if (failureNode.children.has(char)) {
				child.failureLink = failureNode.children.get(char)
				child.output = child.failureLink?.output
					? [...child.output, ...child.failureLink.output]
					: child.output
			} else {
				child.failureLink = root
			}
		}
	}
}

This part is still a bit abstract to me as I’m not yet familiar enough with the breadth-first search algorithm to fully understand or explain what it’s doing. The thing with learning about algorithms, at least for how my brain works, is that it takes time to grasp what the theory means in real life examples and to be able to translate these examples into human-readable code and not just instructions a computer can follow.

3. Searching for patterns

Once we have the functions to create a trie, insert patterns and add failure links, we can have a function that builds a trie from a list of patterns:

function buildTrie(patterns: string[]) {
	const root = createTrie()

	for (const pattern of patterns) {
		insertPattern(root, pattern)
	}

	addFailureLinks(root)

	return root
}

And then create a function to search for these patterns in a text:

function searchTrie(root: TrieNode, text: string) {
	const matches: string[] = []

	let currentNode = root

	for (let i = 0; i < text.length; i++) {
		const char = text[i]

		// if the current node's children do not contain the current
		// character we're looking for, jump to the failure link
		while (currentNode !== root && !currentNode.children.has(char)) {
			if (currentNode.failureLink) {
				currentNode = currentNode.failureLink
			}
		}

		if (currentNode.children.has(char)) {
			currentNode = currentNode.children.get(char)!

			if (currentNode.output.length > 0) {
				matches.push(...currentNode.output)
			}
		}
	}

	return matches
}

Putting it all together:

const patterns = ['cat', 'car', 'cargo', 'dog', 'door']
const trie = buildTrie(patterns)

searchTrie(trie, 'The cat chased the dog through the door with its car')

// [ "cat", "dog", "car" ]

This will return an array of matches: [ 'cat', 'dog', 'door', 'car' ].

Performance

We can use console.time to check how long it takes to perform this search and how that time isn’t negatively affected by adding more patterns to the list:

console.time('buildTrie')
const trie = buildTrie(patterns)
console.timeEnd('buildTrie')

console.time('search')
searchTrie(trie, 'The cat chased the dog through the door with its car')
console.timeEnd('search')

// patterns.length = 5 -> 50
// buildTrie: 0.226ms -> 0.253ms
// search: 0.793ms -> 0.049ms

Conclusion

There are different algorithms that can be used for pattern matching, but the Aho-Corasick is a particularly good option when we need an efficient way of searching multiple patterns simultaneously in a large block of text and it can handle overlapping occurrences well. It requires pre-processing to build the trie and the failure links beforehand, but once that’s done, searching is really fast even when adding more patterns to the trie.

Some other examples where this can be applied in software development are syntax highlighting, a common feature in code editor interfaces, spell checking, and content filtering where we need to identify specific keywords to be blocked or flagged for moderation.

The code from this post can be found at https://github.com/taismassaro/aho-corasick.